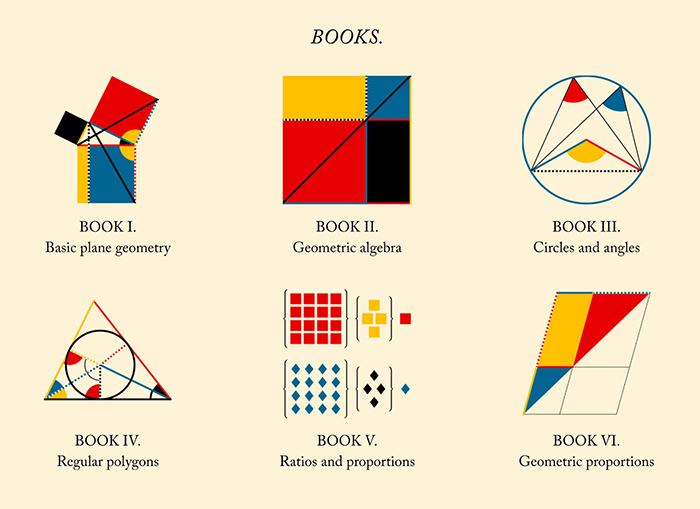
유클리드 기하학은 점, 선, 면과 같은 기본 요소로 공간의 형태와 구조를 해석하려는 일종의  도형학으로서 

그 원리들은 르네상스 시대 원근법의 이론적 토대가 되었다. 

특히 유클리드 기하학이 제시하는 평행선, 비례, 각도에 대한 이해는 

화가들이 3차원 공간을 2차원 화면에 사실적으로 표현하는 데 결정적인 역할을 했다. 

이러한 수학과 예술의 융합은 예술가들을 단순한 기능인이 아닌 지적 창조자로 격상시키는 계기가 되었다.

 1. 세상을 도형으로 이해한다는 것은 어떤 의미인가?

기원전 3세기 유클리드는 같은 물체라도 가까이 있으면 커 보이고 멀리 있으면 작아 보이는 인간 시각의 

불완전성을 지적하며, 자와 컴퍼스를 활용한 기하학 체계화했다. 

기하학은 원래 땅의 경계나 건축물을 정확히 측정하기 위한 실용적인 목적에서 시작되어 

논리적인 학문으로 발전했다. 

즉 현실 세계를 수학적으로 이상화한 점, 선, 면과 같은 기하학적 개념들은 비록 완벽한 형태로 

현실에 존재하지는 않지만, 이를 통해 공간의 논리와 구조를 정확하게 파악할 수 있게 되었다. 

이러한 도형 개념은 우리가 배우는 조형의 기초 이론을 형성하며 세상의 규칙과 본질을 인식하는 도구가 된다. 

반면 원근법은 유클리드 기하학의 원리를 바탕으로 하되, 인간의 시각적 경험을 예술적으로 재해석했다.

 2. 원근법은 어떻게 유클리드 기하학을 예술적으로 확장했는가?

원근법은 유클리드 기하학의 규칙을 따르면서도, 인간의 시각 경험을 반영하여 

새로운 예술 표현의 가능성을 열었다. 

즉 평행선이 소실점에서 만나는 것처럼 보이는 시각적 착시 현상은 원근법의 핵심 원리로, 

이를 통해 그림에 깊이감과 현실감을 부여했다. 

- 평행선과 소실점: 유클리드 기하학에서 평행선은 절대 만나지 않지만, 

원근법은 이 평행선들이 지평선상의 소실점에서 만나는 것처럼 보이는 시각적 현상을 적용했다. 

- 비례와 축척: 유클리드 기하학의 닮음비 개념을 응용하여, 

관찰자로부터의 거리에 따라 대상의 크기가 체계적으로 감소하도록 표현했다. 

이를 통해 2차원 평면에 깊이감을 구현할 수 있게 되었다.